اعداد کوانتومی ‌مغناطیسی مداری

 

 الکترون در اثر نیرویی که از طرف هسته بر آن وارد می‌‌شود، حول هسته می‌‌چرخد. چون الکترون یک ذره باردار است، بنابراین مدار الکترون را می‌‌توان یک مدار مغناطیسی در نظر گرفت. برای این مدار مغناطیسی و در واقع برای الکترون می‌‌توان یک گشتاور دو قطبی مغناطیسی تعریف نمود. این کمیت بر اساس اندازه حرکت زاویه‌ای مداری الکترون تعریف می‌‌شود. یعنی از رابطه μ = eL/2m حاصل می‌‌شود که در آن μ گشتاور دو قطبی مغناطیسی است.

حال اگر یک میدان مغناطیسی خارجی اعمال شود،

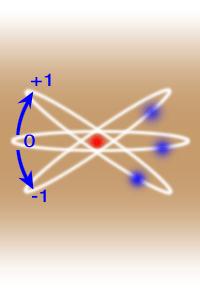
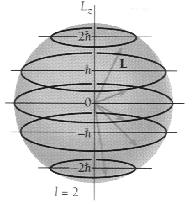
حال اگر یک میدان مغناطیسی خارجی اعمال شود، در این صورت میدان سعی می‌‌کند تا گشتاور دو قطبی مغناطیسی و به تبع آن L را در راستای میدان قرار دهد، اما در مکانیک موجی بردار اندازه حرکت زاویه‌ای مداری L نمی‌‌تواند هر جهتی را نسبت به میدان مغناطیسی اختیار کند، بلکه محدود به جهتهای به خصوصی است که برای آن مؤلفه بردار اندازه حرکت زاویه مداری ، در راستای میدان مغناطیسی ، مضرب دستی از ћ باشد. بنابراین اگر جهت میدان مغناطیسی را در راستای محور z اختیار کنیم، در این صورت مؤلفه z بردار L از رابطه L_z = m_l ћ حاصل می‌‌شود. در این رابطه m_l عدد کوانتومی ‌مغناطیسی مداری است. به ازای یک مقدار مفروض l ، m_l می‌‌تواند مقادیر زیر را اختیار کند:

{m_l ={ l , l - 1 , l - 2 , … , 0 , … , - l

 

اعدد کوانتومی ‌مغناطیسی اسپینی

در نظریه کوانتومی ‌سه ثابت فیزیک کلاسیک مربوط به حرکت ذره‌ای که تحت تأثیر جاذبه عکس مجذوری قرار دارد، کوانتیده‌اند. این سه ثابت عبارتند از: انرژی ، بزرگی اندازه حرکت زاویه‌ای مداری ، مؤلفه اندازه حرکت زاویه‌ای مداری در یک جهت ثابت از فضا. در مکانیک کوانتومی ‌به این ثابتهای حرکت اعداد کوانتومی n و l و m_l نسبت داده می‌‌شوند، اما علاوه بر این سه عدد کوانتومی ، عدد کوانتومی ‌دیگری به نام عدد کوانتومی ‌اسپینی که به مفهوم اسپین الکترون مربوط است، معرفی می‌‌شود.

در سال 1925/1304 گود اسمیت و اوهلن یک اظهار داشتند که یک اندازه حرکت زاویه‌ای ذاتی ، کاملا مستقل از اندازه حرکت زاویه‌ای مداری ، به هر الکترون وابسته است. این اندازه حرکت ذاتی ، اسپین الکترون نامیده می‌‌شود. چون می‌‌توان آن را با اندازه حرکت ذاتی که هر جسم گسترده بر اساس دوران یا اسپین حول مرکز جرم خود دارد، مانسته داشت. البته لازم به توضیح است که در مکانیک موجی تلقی الکترون به عنوان یک کره ساده با بار الکتریکی صحیح نیست، بلکه صرفا به خاطر مشخص کردن اندازه حرکت زاویه‌ای اسپینی الکترون به کمک مدل قابل تجسم ، بهتر است که آن را به عنوان جسمی که در فضا دارای گسترش است و بطور پیوسته حول یک محور به دور خود می‌‌چرخد، فرض کنیم.  

 

مانند اندازه حرکت زاویه‌ای مداری در اینجا نیز می‌‌توانیم یک گشتاور مغناطیسی مربوط به حرکت اسپینی الکترون در نظر بگیریم. چنانچه یک الکترون ، با گشتاور مغناطیسی دائمی خود ، در یک میدان مغناطیسی قرار گیرد، انتظار می‌‌رود که اسپین آن کوانتیده فضایی باشد، یعنی گشتاور مغناطیسی اسپینی و اندازه حرکت زاویه‌ای اسپینی به سمت گیری‌های خاصی محدود خواهند بود.

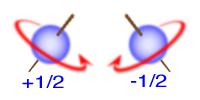
بنابراین اگر میدان مغناطیسی در راستای محور z فرض شود، در این صورت مؤلفه اندازه حرکت زاویه‌ای اسپینی L_sz در جهت این میدان از رابطه L_sz = m_sћ حاصل خواهد شد. در این رابطه m_s عدد کوانتومی ‌مغناطیسی اسپینی نامیده می‌‌شود. از آنجا که الکترون از دسته فرمیونها می‌‌باشد، بنابراین دارای اسپین نیم فرد خواهد بود، لذا عدد کوانتومی m_s فقط می‌‌تواند دو مقدار ممکن 2/1+ و 2/1- را اختیار کند.